Modal Analysis in Parallel
A parallel solver using C++ and LAPACK for proper orthogonal and dynamic mode decomposition using communication reducing tall and skinny QR (TSQR) factorization algorithm
Modal decomposition serves as a valuable tool for understanding complex fluid flow phenomena. It involves breaking down the solution into individual modes or patterns, each representing unique spatial structures or oscillatory behaviors within the flow. This decomposition allows for the identification of dominant patterns, extraction of pertinent information, and potential simplification of flow field representation.
Methods like proper orthogonal decomposition (POD) are commonly employed to filter noise in images and videos or to reduce their size while retaining dominant features. Numerous variations of this algorithm exist, with many online videos providing explanations and demonstrations with interesting examples. One notable application of modal decomposition is in noise reduction.
In my Ph.D. research, which heavily relied on the Direct Simulation Monte Carlo (DSMC) method, noise was a significant factor, especially in scenarios involving linear instabilities like those explored in the Laminar Separation Bubble Instability project. Here, modal decomposition techniques such as proper orthogonal decomposition proved invaluable in understanding the early manifestation of the instabilily.
The POD method involves performing singular value decomposition (SVD) on a matrix, where the rows correspond to the number of solution points and the columns represent the number of temporal snapshots at which the data is captured. In the realm of 3D simulations, the sheer number of simulation points can be substantial; for instance, even my 'coarsest mesh' consisted of millions of computational cells representing spatial variation of solution. Conversely, the number of time snapshots tends to be relatively low, typically on the order of thousands.
This scenario presents a computational challenge: conducting SVD on a matrix that is 'tall and skinny,' meaning it has significantly more rows than columns. Moreover, this operation must be executed in parallel, as the entire matrix cannot be accommodated on a single node of a supercomputer.
To address this challenge, I developed a parallel solver for POD using C++ and the message passing interface (MPI). The solver employs a communication-reducing algorithm known as the Tall and Skinny QR (TSQR) factorization algorithm, developed by Demmel et al.. You can find the implementation on GitHub at the following Github link.
Figure (1) shows an example of using POD to filter DSMC noise (Sawant et al., 2022). The POD-reconstructed data exhibits the same spatial spanwise variation but contains very low statistical noise compared with the DSMC solution. The size of matrix for each flow parameter was 24 million x 400.
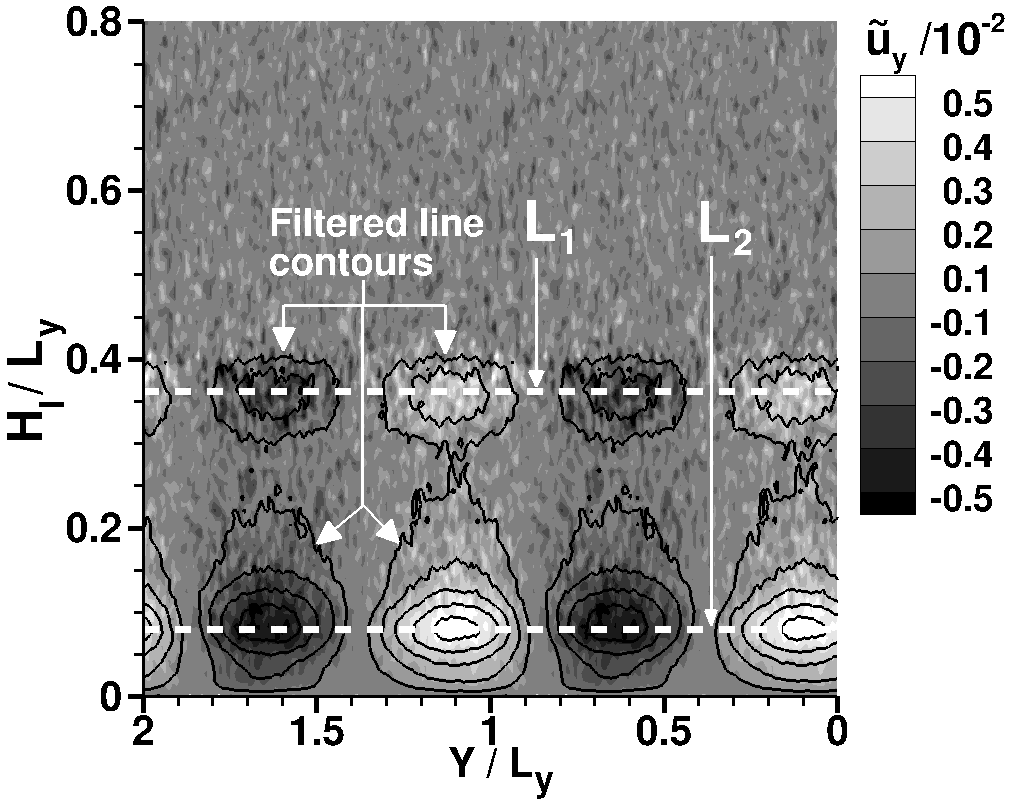
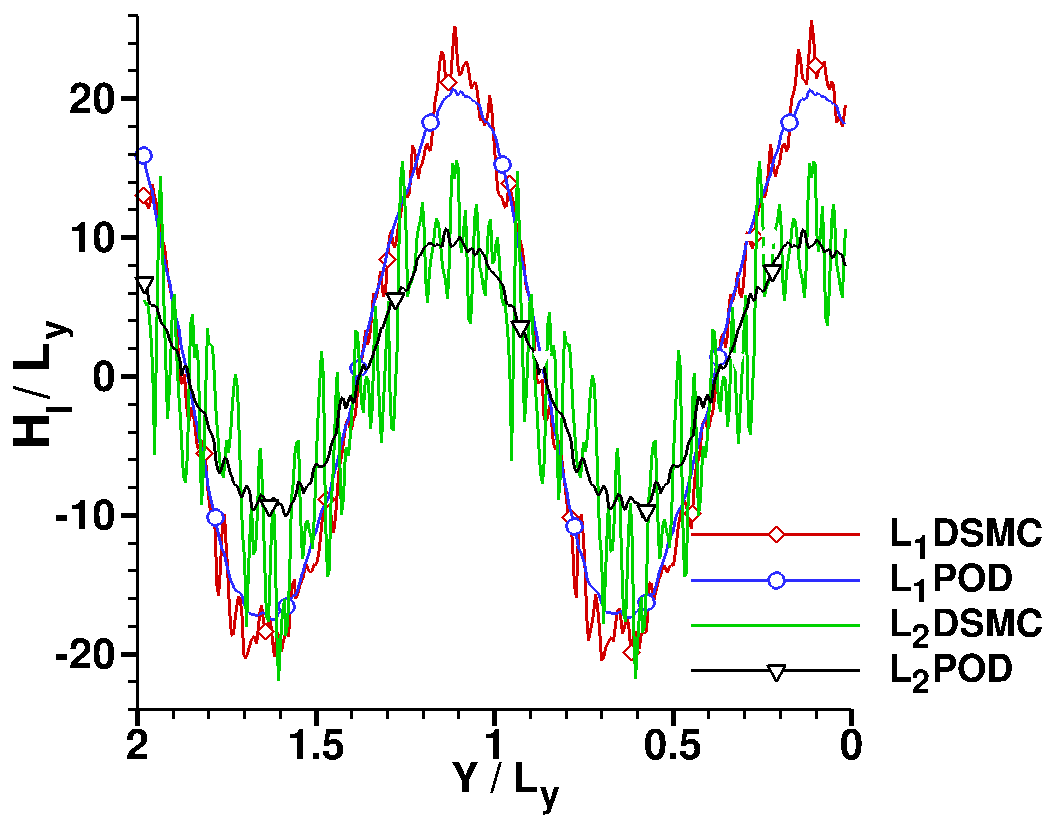
Fig. 1. (a) Contours of raw DSMC field on plane R, defined in Fig. (2) of Laminar Separation Bubble Instability. Overlaid lines are noise-filtered reconstruction of the field using two most dominant POD modes. (b) Comparison of DSMC (unfiltered) and POD (filtered) field along lines L1 and L2 denoted in (a).
The code was further extended to include dynamic mode decomposition (DMD), an algorithm that has been widely utilized since its inception by Schmid, P.J.. Parallelization of this algorithm is described by Sayadi, T. & Schmid, P.J.. However, I never ended up using it in my research. As a validation of my code, consider this example from the book Dynamic Mode Decomposition by Kutz et al.. Let f be composed of two decaying functions, \begin{equation} f_1 = \Re\left[ \text{sech}(x+3) \exp{(-0.1 t + i 2.3t)}\right] \end{equation} \begin{equation} f_2 = \Re\left[ \frac{2 sech(x)}{tanh(x)} \exp{(-0.2t + i 2.8t)}\right] \end{equation} Applying DMD to f for modal decomposition correctly recovers underlying eigenvectors and eigenvalues.
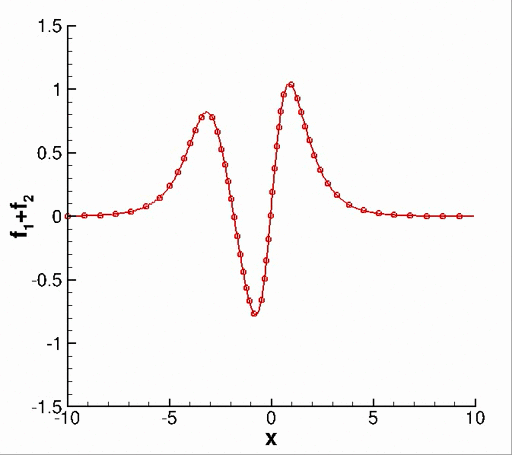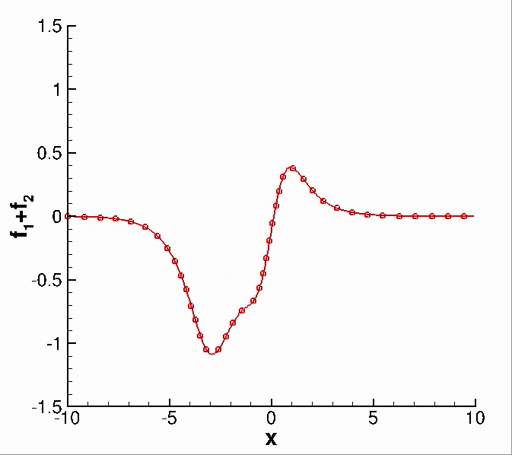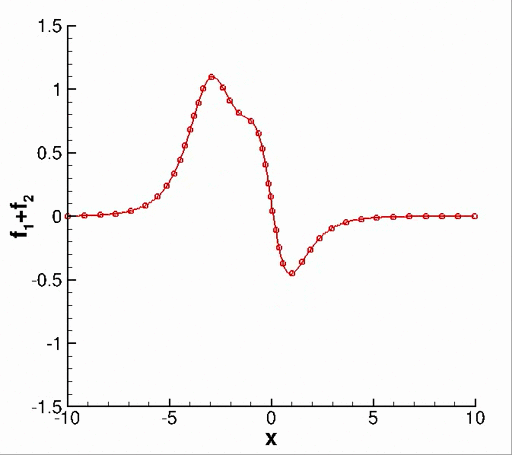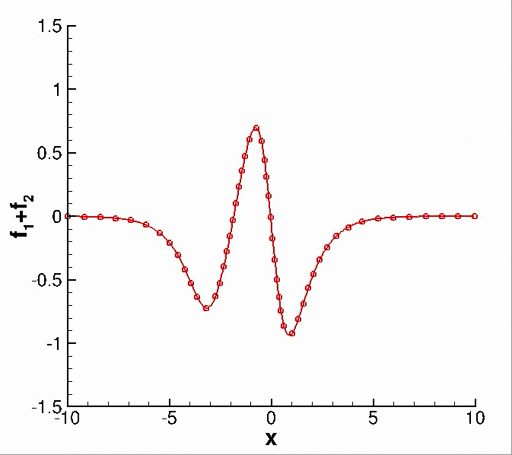
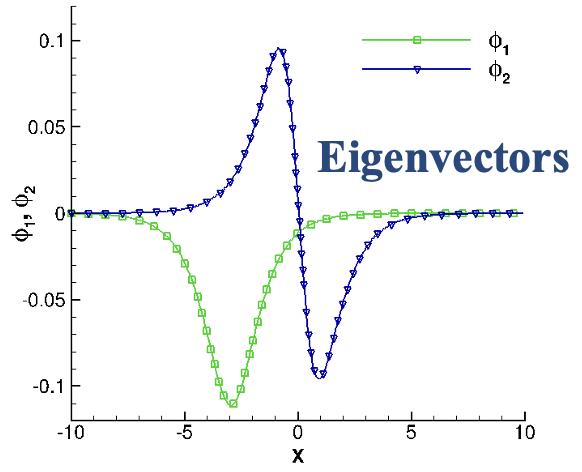
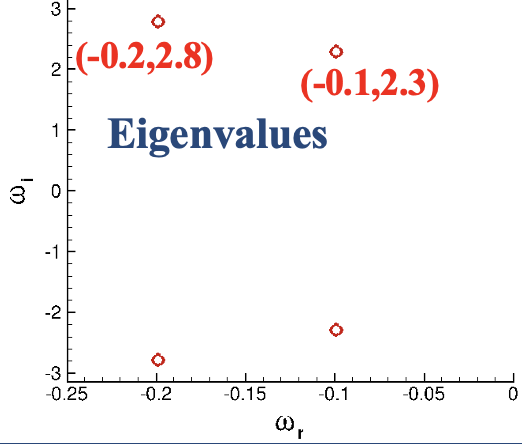
Fig. 1. (a) Function f=f1 + f2. (b) Eigenvectors and (c) continuous time eigenvalues obtained from the DMD algorithm.