Fluctuations in a 1D-shock
Low-frequency fluctuations in the internal structure of 1D shock arising from bimodality of energy density functions
In the study of hypersonic vehicle design, one key question that takes precedence is to understand whether a smooth, laminar flow would transition to turbulence. However, the vast majority of research on this topic focuses on boundary layers, not shocks—a critical element of hypersonic flows.
Linear stability theory has proven highly effective in predicting the stability or instability of boundary layers against small-amplitude disturbances. Yet, predicting the Reynolds number at the transition point remains elusive. Numerous experimental observations have shown a strong correlation between this parameter and the level of freestream noise, which includes atmospheric or tunnel-induced turbulence, acoustic, vorticity, and entropy fluctuations, and particulates. These phenomena collectively fall under the term 'receptivity.'
Numerical investigations into receptivity and natural transition have primarily concentrated on devising models to incorporate freestream disturbances and their interaction with shocks through shock-capturing or shock-fitting methodologies. However, these efforts do not account for accurately resolved shock structures and the intricate molecular fluctuations within their internal non-equilibrium region.
Given that freestream noise inevitably traverses through a shock before engaging with a boundary layer, it becomes imperative to acknowledge the pivotal role of the shock's internal dynamic structure in receptivity investigations. Even in scenarios where the freestream noise remains minimal, comprising solely equilibrium molecular fluctuations, the shock may play a role in transition dynamics due to its interaction with boundary-layer formation at leading edge. Motivated by these considerations, I embarked on a side project during my Ph.D. to explore the nature of fluctuations within simple one-dimensional shocks, using the kinetic Direct Simulation Monte Carlo (DSMC) method, renowned for its precision in modeling shocks.
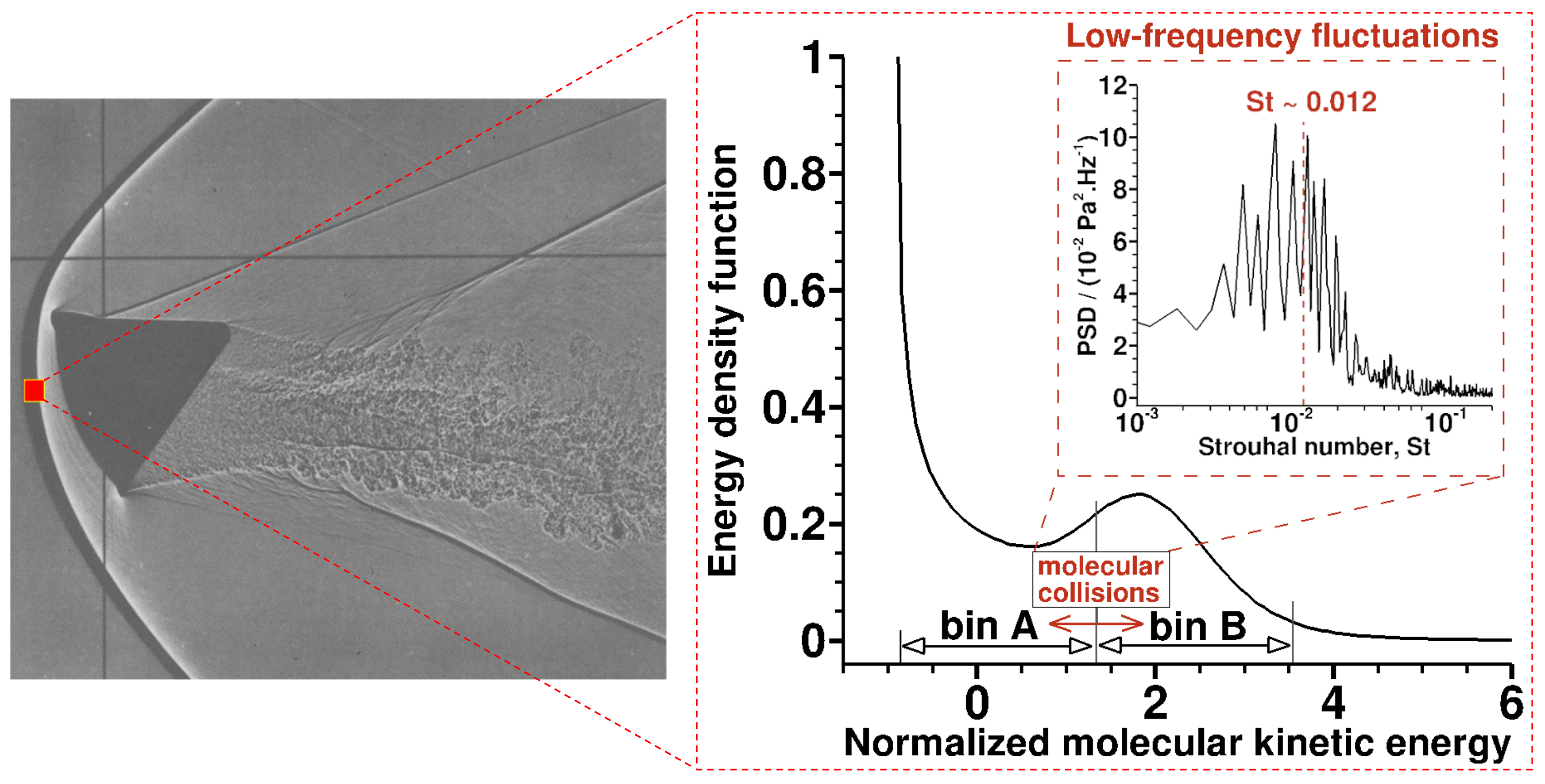
Left: Bow shock seen in NASA's ballistic test over an Apollo like capsule, AOA 25° (taken from Kruse, R. L. (1968) NASA Tech. Note 19680018748.). Right: Bimodal energy density function in a one dimensional shock divided into two *bins* A and B. Collisions between the molecules within these two bins give rise to low-frequency fluctuations 𝑆𝑡 ≈ 0.01.
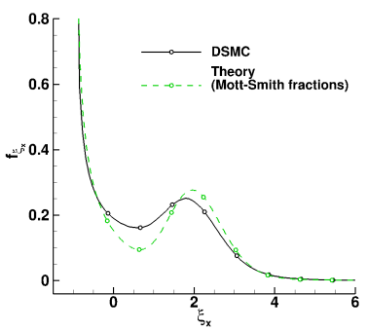
My research resulted in an interesting finding: molecular fluctuations in the internal non-equilibrium region of shock layers exhibit two orders of magnitude lower frequencies than the flow upstream, as depicted in the figure above. The presence of low-frequency fluctuations is shown to be a direct consequence of the bimodal nature of the energy density function of gas particles within the shock.
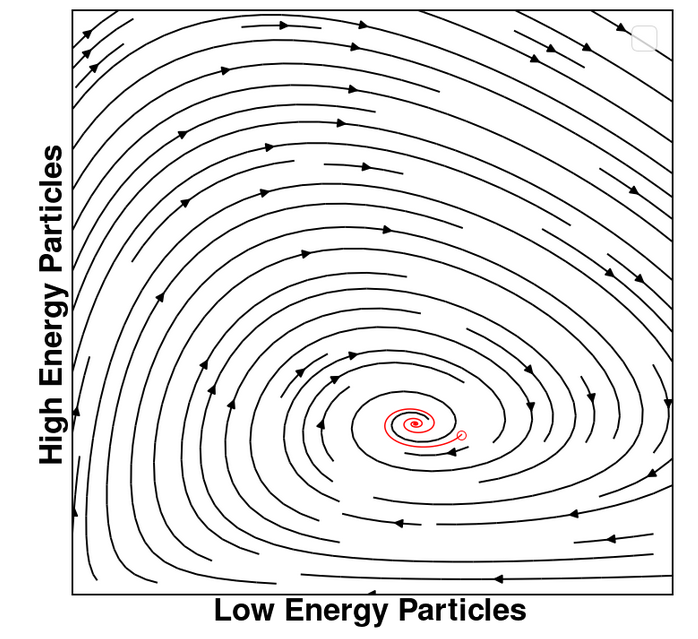
Within the shock layer, we discovered a strong correlation between perturbations in the bimodal probability density function (PDF) and fluctuations in the normal stress. Motivated by this result, I developed a two-energy-bin Lotka-Volterra-type model to describe the reduced-order dynamics of a large number of collision interactions among gas particles.
The model accurately predicts the differences in fluctuation frequencies between the shock and upstream regions. For further details, please refer to (Sawant et al., 2021).
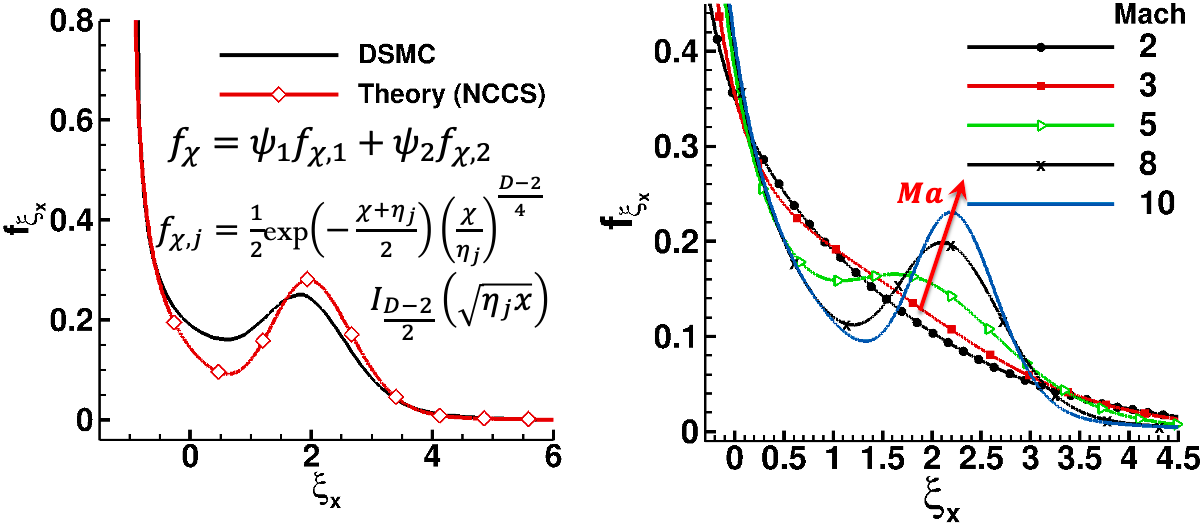
Left: Comparison of theoretically calculated bimodal noncentral χ2 distribution with DSMC for a 1D shock. Right: Variation of these distributions, showing increase in bimodality with increase in Mach number.
Building upon this research, I became intrigued to understand the mathematical form of the bimodal energy density function. I derived probability density functions of particle energies in both the upstream and downstream equilibrium regions, as well as within shocks, revealing that they conform to the shape of non-central χ2 distributions, as illustrated in the figure above.
Subsequently, I established a correlation between the change in the shape of these distributions and the average frequencies observed in shocks obtained from the DSMC simulations. Leveraging these correlations, we developed a semi-empirical relationship capable of predicting the average low-frequency fluctuations in shocks across a broad range of Mach numbers (3 ≤ Ma ≤ 10) and input temperatures (∼90 ≤ Ttr,1 /(K) ≤ 1420), thereby enhancing receptivity analysis.
These interesting findings are described in detail in (Sawant et al., 2022).