Laminar Separation Bubble Instability
Linear Instability of a 3-D Laminar Separation Bubble in Hypersonic (Mach 7) Shock-Wave/Boundary-Layer Interations (SWBLIs)
During my master's and early years of Ph.D., I developed a massively parallel implementation of the Direct Simulation Monte Carlo (DSMC) method for solving the Boltzmann equation of transport, as described in project AMR. In the latter part of my Ph.D., I utilized this solver to model hypersonic shock-wave/boundary-layer interactions (SWBLIs). To understand the significance of SWBLIs in hypersonic research, let me tell you a short story.
On October 3rd, 1967, pilot Pete Knight soared the X15A2 aircraft to a record-breaking Mach number of 6.7 at an altitude of 31 km, equipped with a dummy scramjet. The shock waves from the dummy scramjet impacted the lower ventral fin, causing damage to instrumentation wiring, control gas lines, and even melting bolts used to jettison the scramjet. These ambitious flight tests underscored the critical need for a comprehensive understanding of SWBLIs to master hypersonic flight. Consequently, the study of hypersonic flows over canonical configurations like ramps, wedges, or cones – the foundational elements of hypersonic bodies – has dominated hypersonic research for the past six decades. Recently, efforts have extended to more complex shapes such as double-wedge or double-cone configurations, which yield the most intricate SWBLIs.

Left: X-15 separates from B-52. Right: Damage to lower ventral fin by shock impingement on flight 2-53-97. (taken from Milton Thompson's At the edge of space: The X-15 flight program.)
Returning to our research, we investigated the Mach 7 flow over a 30°-55° double-wedge configuration, yielding SWBLIs teeming with rich physics, as illustrated below. At a freestream unit Reynolds number of 𝑅𝑒=5.2e4/m, this flow exhibits rarefaction effects and shock-thicknesses comparable to the boundary layer's thickness at separation. The DSMC method has proven adept at modeling precise shock structures even under hypersonic conditions, where assumptions inherent in Navier-Stokes equations break down.
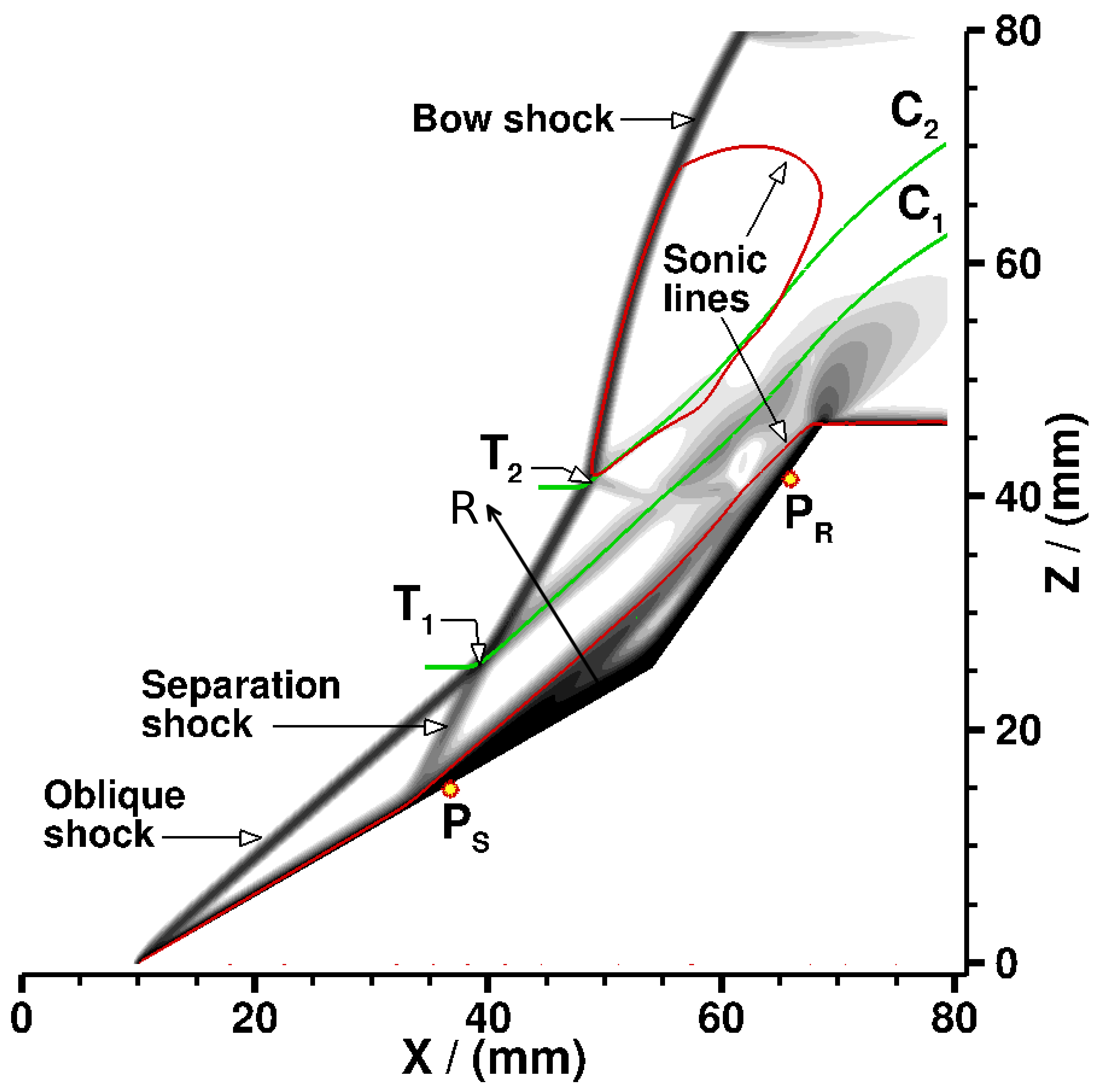
The magnitude of normalized mass density gradient showing shock-wave/boundary-layer interactions in a Mach 7 flow of nitrogen over a double-wedge configuration. T1 and T2 are triple points. Ps and PR are locations where flow separates and reattaches.
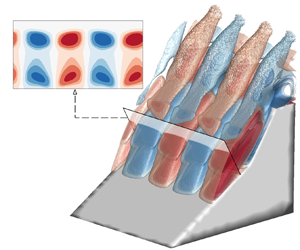
In terms of physics, our focus was on the three-dimensional linear instability of the laminar separation bubble induced by SWBLIs. Interestingly, we discovered that this instability permeates the internal structure of the separation and detached shock layers, manifesting as spanwise-periodic cats-eye patterns in the amplitude functions of all linear flow perturbations. The growth rate and spanwise periodicity length of linear disturbances in the shock layers are found to be identical with those computed within the structures that grow exponentially inside the laminar separation bubble, indicating that the separation and detached shock layers are an integral part of the unstable global mode. Linear amplification of the most unstable three-dimensional flow perturbations leads to synchronization of *low-frequency unsteadiness* of the separation bubble with unsteadiness of the separation- and detached shock layers and the triple point formed at their intersection, with Strouhal number of 𝑆𝑡 ≈ 0.028. These interesting findings are described in detail in (Sawant et al., 2022).
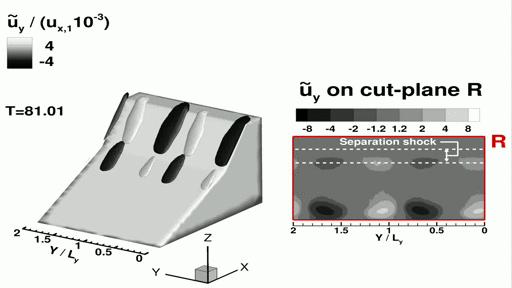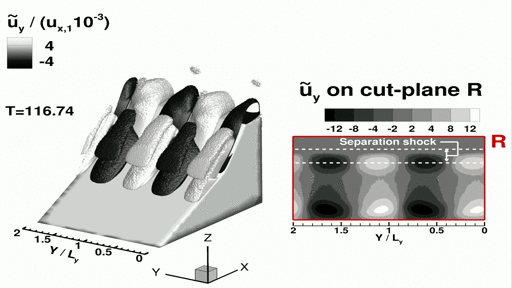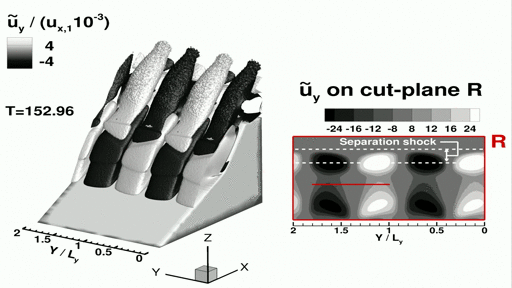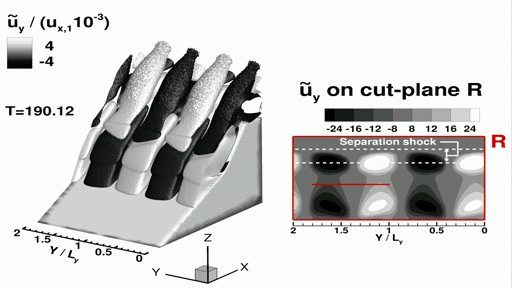
The movie shows spanwise periodic flow structures past the primary separation line observed in the normalized spanwise perturbation velocity. The movie starts playing from T=80, where T is the normalized "through-flow time". The perturbation velocity is zero at the beginning of the simulation, yet over time small scale perturbations occur due to relaxation in the spanwise direction and these sinusoidal structure start to form with increasing magnitude. More importantly, we see that these structures are present inside the separation shock layer!
This flow was modeled using 60 billion computational particles and 4.5 billion adaptively refined computational cells for performing collisions. To accommodate billions of particles and cells, 19.2 k MPI processors were used in this simulation. The spanwise-periodic simulation takes ∼5.5 h per through-flow time (T) using Intel Xeon Platinum 8280 (‘Cascade Lake’) processors of the Frontera supercomputer (2019) and ∼14 h per flow time using Intel Xeon Platinum 8160 (‘Skylake’) processors of the Stampede2 supercomputer (2019). The overall cost of the simulation up to T = 190 required ~870 k node hours (∼43.8 million core hours) of computing time.
(Special thanks to Vassilis Theofilis for his tremendous help in this work.)