Adaptive Mesh Refinement
Adaptive mesh refinement (AMR) strategy with octree grids for the Direct Simulation Monte Carlo (DSMC) method to solve Boltzmann equation of transport
Hypersonic flows (flows over bodies traveling five or more times the speed of sound) exhibit large gradients of macroscopic flow parameters, such as temperature and pressure. To simulate such conditions using Boltzmann equation of transport using a kinetic approach such as the Direct Simulation Monte Carlo (DSMC) method, I lead the development of a C++ solver, known as SUGAR, which is described in (Sawant et al., 2018).
The code takes advantage of message-passing-interface (MPI) for parallel communication between processors, adaptive mesh refinement (AMR) of coarser Cartesian cells to achieve spatial fidelity in regions of strong gradients such as shocks, a cut-cell algorithm to correctly capture physics near embedded surfaces, a domain decomposition strategy based on Morton-Z space-filling-curves, parallel input/output capability, strategies for run-time memory reduction, and inclusion of thermal nonequilibrium models. The code was demonstrated to have 87% weak scaling for a hypersonic flow over a sphere using 8192 Intel Xeon E5-2699v3 processors on NSF’s Bluewaters supercomputer and near-ideal strong scaling speed-up up to 4096 processors. To achieve this good scaling, strategies were implemented that involved accurate estimation of the computational load based on profiled time spent in executing major tasks in DSMC, optimizing point-to-point communication by creating an estimated map of senders and receivers, and optimizing the mapping and introduction of particles into the domain. For this work, I have extensively used scripting languages such as python and bash for data analysis, debugging tools such as Allinea’s Distributed Debugging Tool (DDT), profiling tools such as PerfSuit and Cray Performance Measurement Analysis Tool (CPMAT), memory monitoring tools, and the ‘make’ program building tool.
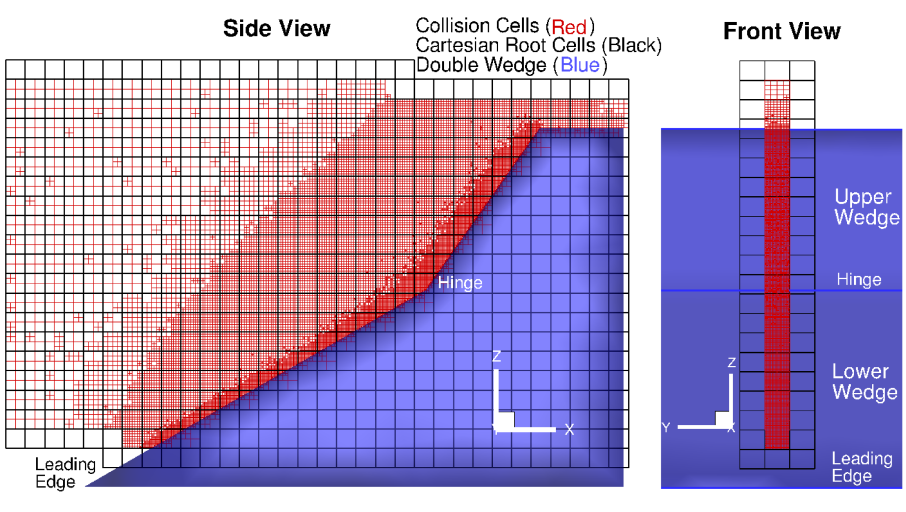
Figure 1. shows the uniform Cartesian grid in black forming root cells, and the AMR grid in red occupied by one of the MPI ranks, for the Mach 7 flow over a double-wedge configuration. Figure 2. illustrates the Morton-based space filling curve strategy for domain partitioning across leaf cells.
Fig. 1. The decomposition of the computational domain held by one of the MPI ranks or processor. It shows two types of grids--black uniform grid representing roots of octree, and adaptively refined unstructured grid used to perform binary collisions of particles. The MPI rank also holds one layer of root grid elements of neighboring processors, called ghost region, for exchange of information.
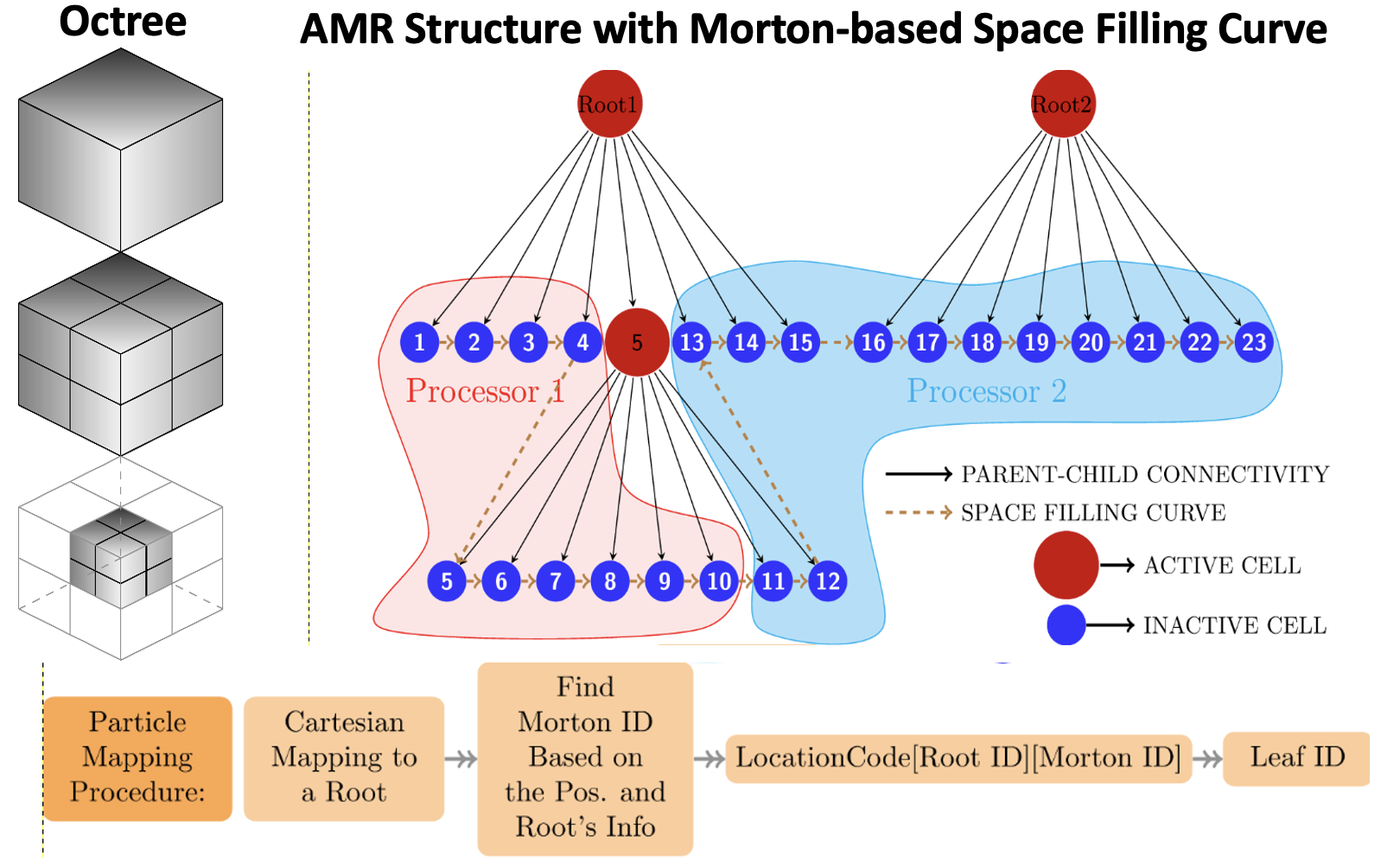
Fig. 2. Sketch on the left shows octree-based AMR hierarchy. AMR occurs on root cells based on the criteria that cell size should be smaller than the local mean free path and there must be sufficient number of particles per cell to perform unbiased collisions. After a series of such refinements, the cells at the lowest level of refinement are called leaf cells. The right side shows Morton-Z based space-filling-curve strategy to allow O(1) access of data in leaf cells, thus eliminating the need of expensive tree traversal.
To facilitate the representation of embedded boundaries, a sophisticated cut-cell algorithm was implemented in the solver and seamlessly integrated with an adaptively refined grid. Accurate determination of collision frequency in DSMC hinges on precise calculation of the fluid volume within each computational cell. The algorithm first detects the cutcells using simple computational geometry algorithms and then reconstructs the polyhedral fluid portion of the computational cell to compute its volume.
Figure 4. illustrates the indentification of cut-cells of an AMR/octree grid embedded with a double-wedge geometry. In this depiction, green cells are perfect cut-cells, meaning that part of these cells lie on the fluid side, while the other part inside the embedded geometry. Conversely, the red cells exhibit faces that are co-planar with triangular edges of the geometry panels. The blue cells, on the other hand, encompass those that are not cut-cells or those that are co-planar with triangulated panels without having any of the panel edges passing through their faces.
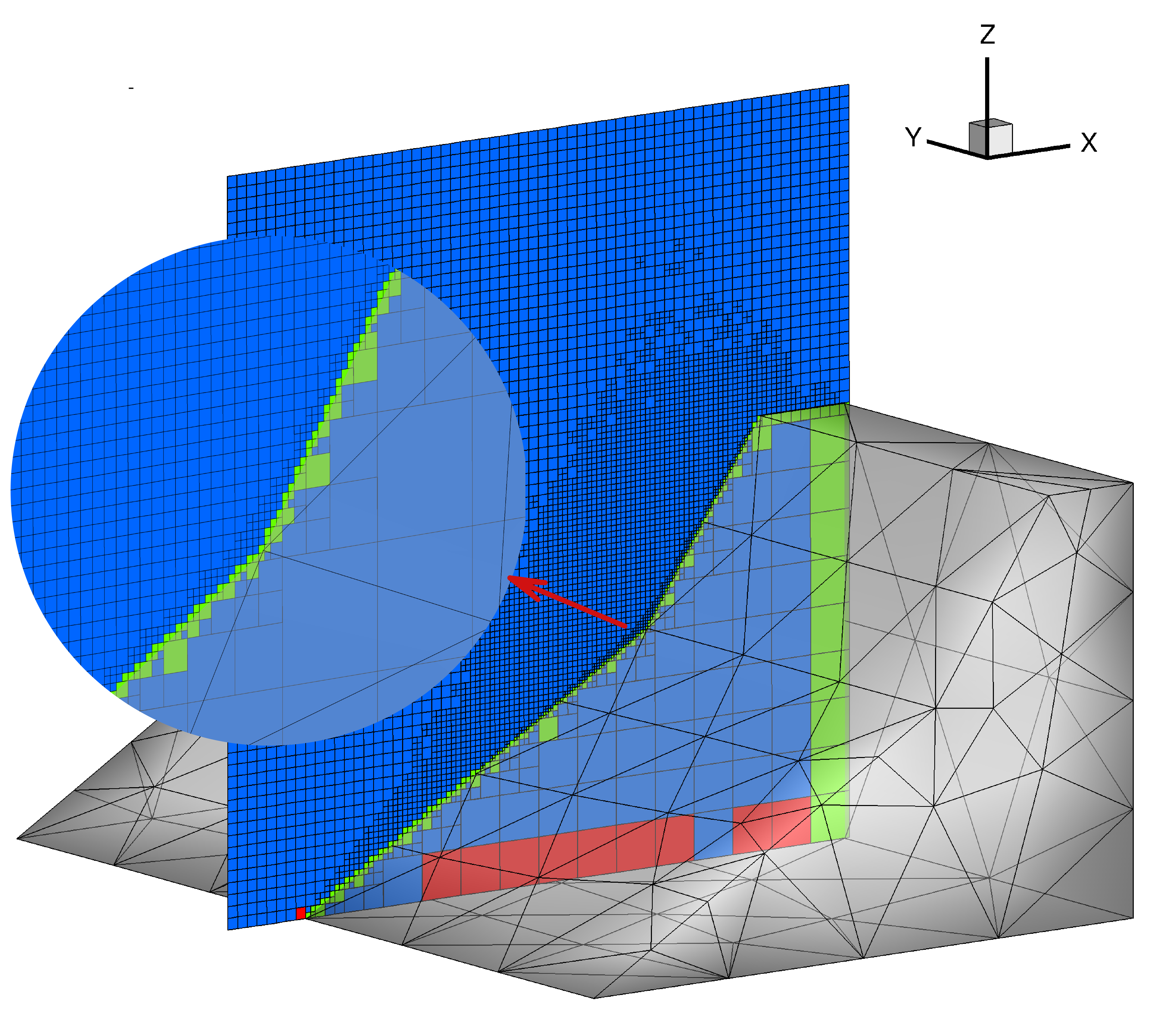
Fig. 3. The cut-cells formed through the intersection of triangulated embedded boundary and leaf cells of AMR/octree grid.